What are CTF Contests..?
Capture The Flag (CTF) contest is a special kind of cybersecurity competition designed to challenge its participants to solve computer security problems and/or capture and defend computer systems.
What should we do in CTF contest’s.?
We need to solve the challenge and submit the flag based on hints.
Categories in the Capture the Flag
- Reverse Engineering
- cryptography
- Web
- Misc
- Steganography
- Binary Analysis
- Forensics
- Programming
In the Cryptography category we will have RSA related challanges.
What is RSA?
RSA (Rivest–Shamir–Adleman) is one of the first public-key cryptosystems encryption which is widely used for secure data transmission.
RSA ALGORITHM
It contains 3 parts
part1: Key Generation
Select p,q p and q are prime numbers; p!=q
Calculate n n = p * q
Calculate phi(ϕ) ϕ = ( p - 1 ) * ( q - 1 )
Select integer e GCD ( ϕ(n) , e ) = 1; 1 < e < ϕ(n)
Calculate d d = inverse(e) % ϕ(n)
Public Key (Pk) {e,n}
Private Key (Pr) {d,n}
Part2: Encryption
Plain Text (M) M < n
Cipher Text (C) C = pow( M , e) % n
Part3: Decryption
Cipher Text (C) C
Plain Text (M) M = pow(C , d) % n
Solving Problems
I have taken some problems from the CTF’s and show you how to solve RSA related challenges in the CTF’s.
Here the challanges are from the Capture the flag learn website.
Challange Name: RSA Beginner
Question:
I found this scribbled on a piece of paper. Can you make sense of it? https://mega.nz/#!zD4wDYiC!iLB3pMJElgWZy6Bv97FF8SJz1KEk9lWsgBSw62mtxQg
Solution:
Open the given link and see the details. In this link we will have something like this, By seeing this we can directly conclude these numbers are related to RSA algorithm.
e: 3 c:219878849218803628752496734037301843801487889344508611639028 n: 24584123651247885275290973491257558181596763003304983826908
Here they have given n,e,c (cipher text). We have to decode this cipher text using RSA.
According to the RSA algorithm, we need to have the p,q values. As p,q should be prime numbers from n we can find the prime factors of n. Here I am using http://factordb.com/ to find the factors for the n.
Goto here and paste the n value and click on factorize you will get the factors and assign those factors to the p,q.
we got all the details that we need so we need to find the plain text from the ciphertext. Here I have written a python code for decoding the ciphertext.
from Crypto.Util.number import inverse
n=245841236512478852752909734912575581815967630033049838269083
e=3
c=219878849218803628752496734037301843801487889344508611639028
p=416064700201658306196320137931
q=590872612825179551336102196593
phi=(p-1)*(q-1)
#calculating phi
d=inverse(e,phi)
#calculating d
m=pow(c,d,n)
#decoding ciphertext; i.e: M = pow(C , d) % n
print(hex(m)[2:-1].decode("hex"))
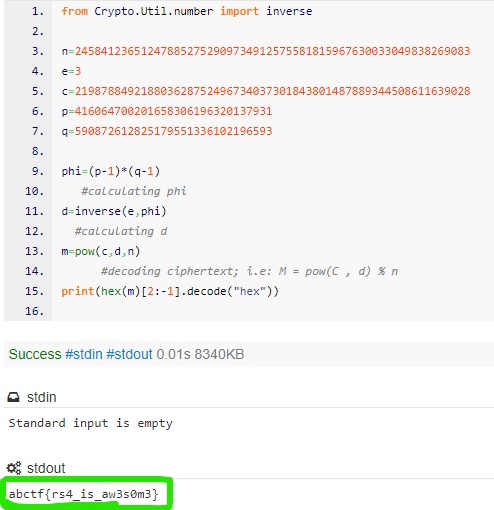
So you see here’s the flag..!
Challange2: CoppeRSA Lattice
Question:
There are plenty of bits of randomness in the key. This has to be secure!
I am so confident, that I am sharing a snippet of my implementation:
import random base = random.getrandbits(2048)
p = next_prime(base + random.getrandbits(256))
q = next_prime(base + random.getrandbits(256))
n = p * q
e = 65537
print("e = ", e)
print("n = ", n)
c = power_mod(m, e, n)
print("c = ", c)
Output:
e = 65537
n = 8281850967132278399574272688766937486036646313403007679588335903785669628431708760927341727806006769095252325575815709840401878674105658204057327337750902945521512357960818523078486774689928139816732080923197367563639383252762498921096166065153092144335239373370093976823925031794323976150363874930075228846801224430767428594024165529140949082062667410186456029480046489969338885725614510660737026927443934115006027747874368836800022473917576424175601374800697491622086825964475396316066082109998646438504664272000556702241576240616765962934452557847306066736505798267513078073147161755828577875047115978481485076227911405625234425533967247248864837854031634968764570599279385827285321806293661331225163255461894680337693227417748934924109356565823327149859245521513696171473417470936260563397398387972467438182651142096935931112668743912944902147582538985769095457203775208567489073198557073226907349118348902079942096374377432431441166710584381655348979330535397040250376989291669788189409825278457889980676574146044704329826483808929549888234303934178478274711686806257841293265249466735277673158607466360053037971774844824065612178793324128914371112619033111301900922374201703477207948412866443213080633623441392016518823291181
c = 6407923537926201847312357068295079879508779752068254604904486842729636773279241546432035102141932853761974844472828552921133743850412718722424893044377874567625621282274625365299685502104113862870672461666586814138206797733946319875258776059721304226419810313489197076949529322847815009706727586961448584443159011118432142946962961532154723891985416387650240762711716865116844837968079333914181751979527853152286708153252001832721723040664452442266930832118353632114958540067674924812749763008217133300059446967170825813909142247660230309955433005706793802514554628379255160648976960069078223370104177403453404917998945232459801324103878906593528309460372271638119657797804398399482025063414403804134607772871958848100256643503372624214762343403925077455660522664025602043433142314759978192969519687720668535544914589329155338178120703060384042066182354031274600184116143293639032906542194564776766076911767759167772137229504115598174156646085123675283692418970988032320780636742598466655712520383055569607154074137271584433653335176877094399371749081016317705026349554938167377640856287458145646649292278971980553895419112860061073864077521131958519819285117031990498977039003918710661660868949818362940359852436185282868088342132Solution:
They have given e,n,c values, we have tofind the remaining values.
According to the RSA algorithm, we need to have the p,q values. As p,q should be prime numbers from n we can find the prime factors of n. Here I am using http://factordb.com/ to find the factors for the n.
Goto here and paste the n value and click on factorize you will get the factors and assign those factors to the p,q.
we got all the details that we need so we need to find the plain text from the ciphertext. Here I have written a python code for decoding the ciphertext.
from Crypto.Util.number import inverse
p = 2877820523787450925749443223409676535526103461002156158445828224293671401993991478543020287097392331073352851877283061169200661485601861126177989029099279726556037706157577055235829106587295127330817726845862915284936240880512882371822435354503703582818585826639860414460347276612398615213473473435297607044419660432857760267782763215613805061134548930946450808892523918406477350229326879718460875896139320212120566207583969498664502640043503068067423704342779684140776844591504545219651693576024138161226306265777913216051021635043708034933142150577361241126706252795462441428424206966514776010058207246337809108763
q = 2877820523787450925749443223409676535526103461002156158445828224293671401993991478543020287097392331073352851877283061169200661485601861126177989029099279726556037706157577055235829106587295127330817726845862915284936240880512882371822435354503703582818585826639860414460347276612398615213473473435297607044419660432857760267782763215613805061134548930946450808892523918406477350229326879718460875896139320212120566207583969498664502640043503068067423704342779684140776844591504545219651693576024138161226306265777913216051021635043708034966478921186010140653104995611058414645030602000549187384764408555794028217687
n = p * q
e = 65537
c = 6407923537926201847312357068295079879508779752068254604904486842729636773279241546432035102141932853761974844472828552921133743850412718722424893044377874567625621282274625365299685502104113862870672461666586814138206797733946319875258776059721304226419810313489197076949529322847815009706727586961448584443159011118432142946962961532154723891985416387650240762711716865116844837968079333914181751979527853152286708153252001832721723040664452442266930832118353632114958540067674924812749763008217133300059446967170825813909142247660230309955433005706793802514554628379255160648976960069078223370104177403453404917998945232459801324103878906593528309460372271638119657797804398399482025063414403804134607772871958848100256643503372624214762343403925077455660522664025602043433142314759978192969519687720668535544914589329155338178120703060384042066182354031274600184116143293639032906542194564776766076911767759167772137229504115598174156646085123675283692418970988032320780636742598466655712520383055569607154074137271584433653335176877094399371749081016317705026349554938167377640856287458145646649292278971980553895419112860061073864077521131958519819285117031990498977039003918710661660868949818362940359852436185282868088342132
phi=(p-1)*(q-1)
d=inverse(e,phi)
m=pow(c,d,n)
print(hex(m)[2:-1].decode("hex"))
So finally we got the flag. Like this we can solve rsa challenges in ctf.
Here is how RSA problem is given in the inctf202:
challenge3: PolyRSA
This is one of the writeup from the inctf. I am unable to solve this challenge at that time.
For this challenge we were given a single file out.txt which contains commands used in sage interactive shell and there output.
In the out.txt file we have, three values
- p = 2470567871 (a prime number)
- n = … (a 255 degree polynomial)
- c = m ^ 65537 (also a polynomial)
These parameters constitute the RSA Encryption but instead of Group of numbers modulo n, this uses univariate polynomials over the finite field Zp.
Use the following resource to understand about this
Polynomial based RSA
As in integer group, we have to find the multiplicative order of the group formed by residue polynomials of given n.
Above resource specifies the formula in page 14 ass = (p**d1 - 1) * (p**d2 - 1) where d1 and d2 are the degrees of irreducible polynomials constituing the given modulus(n).
After obtaining s (multiplicative order), finding the inverse of e = 65537 and raising the ct polynomial to the inverse gives the message polynomial.
Converting the coefficients of message polynomial gives us the flag.
q1, q2 = n.factor() q1, q2 = q1[0], q2[0] s = (p**q1.degree() - 1) * (p**q2.degree() - 1) assert gcd(e, s) == 1 d = inverse_mod(e, s) m = pow(c, d, n) flag = bytes(m.coefficients())
p = 2470567871
P = PolynomialRing(Zmod(p), name = 'x')
x = P.gen()
e = 65537
n = 1932231392*x^255 + 1432733708*x^254 + 1270867914*x^253 + 1573324635*x^252 + 2378103997*x^251 + 820889786*x^250 + 762279735*x^249 + 1378353578*x^248 + 1226179520*x^247 + 657116276*x^246 + 1264717357*x^245 + 1015587392*x^244 + 849699356*x^243 + 1509168990*x^242 + 2407367106*x^241 + 873379233*x^240 + 2391647981*x^239 + 517715639*x^238 + 828941376*x^237 + 843708018*x^236 + 1526075137*x^235 + 1499291590*x^234 + 235611028*x^233 + 19615265*x^232 + 53338886*x^231 + 434434839*x^230 + 902171938*x^229 + 516444143*x^228 + 1984443642*x^227 + 966493372*x^226 + 1166227650*x^225 + 1824442929*x^224 + 930231465*x^223 + 1664522302*x^222 + 1067203343*x^221 + 28569139*x^220 + 2327926559*x^219 + 899788156*x^218 + 296985783*x^217 + 1144578716*x^216 + 340677494*x^215 + 254306901*x^214 + 766641243*x^213 + 1882320336*x^212 + 2139903463*x^211 + 1904225023*x^210 + 475412928*x^209 + 127723603*x^208 + 2015416361*x^207 + 1500078813*x^206 + 1845826007*x^205 + 797486240*x^204 + 85924125*x^203 + 1921772796*x^202 + 1322682658*x^201 + 2372929383*x^200 + 1323964787*x^199 + 1302258424*x^198 + 271875267*x^197 + 1297768962*x^196 + 2147341770*x^195 + 1665066191*x^194 + 2342921569*x^193 + 1450622685*x^192 + 1453466049*x^191 + 1105227173*x^190 + 2357717379*x^189 + 1044263540*x^188 + 697816284*x^187 + 647124526*x^186 + 1414769298*x^185 + 657373752*x^184 + 91863906*x^183 + 1095083181*x^182 + 658171402*x^181 + 75339882*x^180 + 2216678027*x^179 + 2208320155*x^178 + 1351845267*x^177 + 1740451894*x^176 + 1302531891*x^175 + 320751753*x^174 + 1303477598*x^173 + 783321123*x^172 + 1400145206*x^171 + 1379768234*x^170 + 1191445903*x^169 + 946530449*x^168 + 2008674144*x^167 + 2247371104*x^166 + 1267042416*x^165 + 1795774455*x^164 + 1976911493*x^163 + 167037165*x^162 + 1848717750*x^161 + 573072954*x^160 + 1126046031*x^159 + 376257986*x^158 + 1001726783*x^157 + 2250967824*x^156 + 2339380314*x^155 + 571922874*x^154 + 961000788*x^153 + 306686020*x^152 + 80717392*x^151 + 2454799241*x^150 + 1005427673*x^149 + 1032257735*x^148 + 593980163*x^147 + 1656568780*x^146 + 1865541316*x^145 + 2003844061*x^144 + 1265566902*x^143 + 573548790*x^142 + 494063408*x^141 + 1722266624*x^140 + 938551278*x^139 + 2284832499*x^138 + 597191613*x^137 + 476121126*x^136 + 1237943942*x^135 + 275861976*x^134 + 1603993606*x^133 + 1895285286*x^132 + 589034062*x^131 + 713986937*x^130 + 1206118526*x^129 + 311679750*x^128 + 1989860861*x^127 + 1551409650*x^126 + 2188452501*x^125 + 1175930901*x^124 + 1991529213*x^123 + 2019090583*x^122 + 215965300*x^121 + 532432639*x^120 + 1148806816*x^119 + 493362403*x^118 + 2166920790*x^117 + 185609624*x^116 + 184370704*x^115 + 2141702861*x^114 + 223551915*x^113 + 298497455*x^112 + 722376028*x^111 + 678813029*x^110 + 915121681*x^109 + 1107871854*x^108 + 1369194845*x^107 + 328165402*x^106 + 1792110161*x^105 + 798151427*x^104 + 954952187*x^103 + 471555401*x^102 + 68969853*x^101 + 453598910*x^100 + 2458706380*x^99 + 889221741*x^98 + 320515821*x^97 + 1549538476*x^96 + 909607400*x^95 + 499973742*x^94 + 552728308*x^93 + 1538610725*x^92 + 186272117*x^91 + 862153635*x^90 + 981463824*x^89 + 2400233482*x^88 + 1742475067*x^87 + 437801940*x^86 + 1504315277*x^85 + 1756497351*x^84 + 197089583*x^83 + 2082285292*x^82 + 109369793*x^81 + 2197572728*x^80 + 107235697*x^79 + 567322310*x^78 + 1755205142*x^77 + 1089091449*x^76 + 1993836978*x^75 + 2393709429*x^74 + 170647828*x^73 + 1205814501*x^72 + 2444570340*x^71 + 328372190*x^70 + 1929704306*x^69 + 717796715*x^68 + 1057597610*x^67 + 482243092*x^66 + 277530014*x^65 + 2393168828*x^64 + 12380707*x^63 + 1108646500*x^62 + 637721571*x^61 + 604983755*x^60 + 1142068056*x^59 + 1911643955*x^58 + 1713852330*x^57 + 1757273231*x^56 + 1778819295*x^55 + 957146826*x^54 + 900005615*x^53 + 521467961*x^52 + 1255707235*x^51 + 861871574*x^50 + 397953653*x^49 + 1259753202*x^48 + 471431762*x^47 + 1245956917*x^46 + 1688297180*x^45 + 1536178591*x^44 + 1833258462*x^43 + 1369087493*x^42 + 459426544*x^41 + 418389643*x^40 + 1800239647*x^39 + 2467433889*x^38 + 477713059*x^37 + 1898813986*x^36 + 2202042708*x^35 + 894088738*x^34 + 1204601190*x^33 + 1592921228*x^32 + 2234027582*x^31 + 1308900201*x^30 + 461430959*x^29 + 718926726*x^28 + 2081988029*x^27 + 1337342428*x^26 + 2039153142*x^25 + 1364177470*x^24 + 613659517*x^23 + 853968854*x^22 + 1013582418*x^21 + 1167857934*x^20 + 2014147362*x^19 + 1083466865*x^18 + 1091690302*x^17 + 302196939*x^16 + 1946675573*x^15 + 2450124113*x^14 + 1199066291*x^13 + 401889502*x^12 + 712045611*x^11 + 1850096904*x^10 + 1808400208*x^9 + 1567687877*x^8 + 2013445952*x^7 + 2435360770*x^6 + 2414019676*x^5 + 2277377050*x^4 + 2148341337*x^3 + 1073721716*x^2 + 1045363399*x + 1809685811
c = 1208612545*x^254 + 1003144104*x^253 + 1173365710*x^252 + 1528252326*x^251 + 2263767409*x^250 + 2030579621*x^249 + 820048372*x^248 + 1474305505*x^247 + 1313951805*x^246 + 191260021*x^245 + 687901467*x^244 + 231907128*x^243 + 1757265648*x^242 + 1536859261*x^241 + 97792274*x^240 + 86150615*x^239 + 2283802022*x^238 + 728791370*x^237 + 1402241073*x^236 + 2010876897*x^235 + 1112960608*x^234 + 1785301939*x^233 + 862124720*x^232 + 573190801*x^231 + 1353395115*x^230 + 1041912948*x^229 + 1592516519*x^228 + 2043096090*x^227 + 970437868*x^226 + 945296597*x^225 + 764979415*x^224 + 151795004*x^223 + 744776063*x^222 + 49064457*x^221 + 379720326*x^220 + 549708067*x^219 + 1278937325*x^218 + 1348751857*x^217 + 897039278*x^216 + 1738651055*x^215 + 1458044806*x^214 + 947593966*x^213 + 604294495*x^212 + 1101712128*x^211 + 1106608879*x^210 + 556697284*x^209 + 339078898*x^208 + 135886774*x^207 + 682237064*x^206 + 1298394254*x^205 + 2038363686*x^204 + 1138996508*x^203 + 321551693*x^202 + 1194023535*x^201 + 1627100598*x^200 + 581786959*x^199 + 209400153*x^198 + 1354413890*x^197 + 1689568849*x^196 + 1038349567*x^195 + 2129265853*x^194 + 96150366*x^193 + 1879712323*x^192 + 140146576*x^191 + 855348682*x^190 + 571231503*x^189 + 1759489757*x^188 + 1528175919*x^187 + 1420729777*x^186 + 1778060705*x^185 + 204520875*x^184 + 2409946047*x^183 + 1703900286*x^182 + 379350638*x^181 + 145936788*x^180 + 644037909*x^179 + 946490870*x^178 + 2143460817*x^177 + 2124654819*x^176 + 735909283*x^175 + 1956333192*x^174 + 69508572*x^173 + 1998473705*x^172 + 2219097711*x^171 + 2324764950*x^170 + 1295835297*x^169 + 475763021*x^168 + 124896627*x^167 + 392652227*x^166 + 2414019050*x^165 + 519556546*x^164 + 2379934828*x^163 + 74942046*x^162 + 2333943359*x^161 + 5807728*x^160 + 1572302913*x^159 + 933057583*x^158 + 2327572070*x^157 + 2174172163*x^156 + 326654947*x^155 + 2362777406*x^154 + 1571381551*x^153 + 818720017*x^152 + 564409161*x^151 + 784212625*x^150 + 2084631116*x^149 + 1709163682*x^148 + 1791572159*x^147 + 2362306858*x^146 + 1870950847*x^145 + 936293454*x^144 + 1992907305*x^143 + 2427866610*x^142 + 1377299939*x^141 + 2336147340*x^140 + 419537038*x^139 + 1775945090*x^138 + 1084486367*x^137 + 1628708302*x^136 + 624109245*x^135 + 1140675451*x^134 + 848915999*x^133 + 1380203834*x^132 + 103496883*x^131 + 81739774*x^130 + 2055692293*x^129 + 1586687843*x^128 + 1682316161*x^127 + 134734383*x^126 + 885001299*x^125 + 2466212723*x^124 + 137905246*x^123 + 2305925724*x^122 + 410043787*x^121 + 2154453335*x^120 + 2018367068*x^119 + 1967315089*x^118 + 220606010*x^117 + 1066579186*x^116 + 2022385524*x^115 + 1564928688*x^114 + 851080667*x^113 + 1683812556*x^112 + 672848621*x^111 + 646553151*x^110 + 1348955204*x^109 + 1543570099*x^108 + 2260622184*x^107 + 1111757240*x^106 + 1797688791*x^105 + 1307761272*x^104 + 179896670*x^103 + 1197947306*x^102 + 1792231092*x^101 + 1515817157*x^100 + 1510541452*x^99 + 1784535666*x^98 + 1755403646*x^97 + 2388416288*x^96 + 1913808879*x^95 + 2139772089*x^94 + 1373043969*x^93 + 900021127*x^92 + 1613888837*x^91 + 331160696*x^90 + 2404083812*x^89 + 448818904*x^88 + 592910594*x^87 + 2436296390*x^86 + 2103089380*x^85 + 2027661376*x^84 + 277165788*x^83 + 717390488*x^82 + 319876555*x^81 + 1394843317*x^80 + 2314542109*x^79 + 2295617403*x^78 + 313842193*x^77 + 1918458371*x^76 + 1189324530*x^75 + 1765150225*x^74 + 1107038066*x^73 + 613811679*x^72 + 578744934*x^71 + 538203467*x^70 + 1710976133*x^69 + 1681208001*x^68 + 462043988*x^67 + 299437516*x^66 + 1843758398*x^65 + 851754779*x^64 + 1850189150*x^63 + 710529550*x^62 + 922473306*x^61 + 2344816934*x^60 + 54182289*x^59 + 2394694981*x^58 + 1849818608*x^57 + 1926799414*x^56 + 950266030*x^55 + 1290713338*x^54 + 1851455277*x^53 + 1607851092*x^52 + 1587576465*x^51 + 2279226257*x^50 + 1637387507*x^49 + 779327218*x^48 + 919124653*x^47 + 1126060258*x^46 + 2304179492*x^45 + 77984480*x^44 + 966167063*x^43 + 402292668*x^42 + 1332816563*x^41 + 524746316*x^40 + 2427530022*x^39 + 677075099*x^38 + 755256194*x^37 + 2152433299*x^36 + 2197374397*x^35 + 2290208129*x^34 + 996810109*x^33 + 101994796*x^32 + 252415814*x^31 + 1964967972*x^30 + 1533782356*x^29 + 1034980624*x^28 + 816216163*x^27 + 1535614986*x^26 + 1835762944*x^25 + 1147606118*x^24 + 1189426347*x^23 + 33594119*x^22 + 2113251273*x^21 + 826059142*x^20 + 1074101610*x^19 + 1638140405*x^18 + 1633380033*x^17 + 2005588694*x^16 + 2087514746*x^15 + 768034353*x^14 + 104476320*x^13 + 483234608*x^12 + 2424146196*x^11 + 49841203*x^10 + 145673059*x^9 + 705090263*x^8 + 1832451737*x^7 + 2394175351*x^6 + 1966712784*x^5 + 276537935*x^4 + 499607533*x^3 + 1981107449*x^2 + 776654074*x + 886398299
q1, q2 = n.factor()
q1, q2 = q1[0], q2[0]
s = (p**q1.degree() - 1) * (p**q2.degree() - 1)
assert gcd(e, s) == 1
d = inverse_mod(e, s)
m = pow(c, d, n)
flag = bytes(m.coefficients())
print("[+] Flag :: ", flag.decode())